VaR ( Value at Risk ) là gì? Những phương pháp ước tính cùng ưu nhược điểm
02/07/2022
Đăng bởi: Hà Thu
Giá trị chịu rủi ro là một công cụ thống kê và đo lường mức độ rủi ro tài chính, danh mục đầu tư hay vị thế nắm giữ trong quãng thời gian cụ thể của công ty.
Để hiểu rõ hơn về VaR cũng như những phương pháp ước tính, bạn đọc hãy cùng chuyên trang khám phá chủ đề thú vị này qua bài viết hôm nay.
Giải thích VaR và ví dụ minh họa
Trong tiếng Anh, giá trị rủi ro được gọi là Value at Risk(viết tắt: VaR). Như đã nhắc đến trước đó, đây là một công cụ được sử dụng để đo lường, định lượng mức độ rủi ro tài chính, danh mục đầu tư hoặc tình trạng nắm giữ trong quãng thời gian nào đó.

Trong tiếng Anh, giá trị rủi ro được gọi là Value at Risk
Khái niệm được sử dụng vô cùng rộng rãi ở các ngân hàng đầu tư và thương mại nhằm xác định mức độ và tỉ lệ tổn thất có khả năng xảy ra.
Giá trị này có thể áp dụng tính toán cho từng vị thế cụ thể, hay toàn bộ danh mục đầu tư, hoặc mức độ rủi ro đối với toàn công ty.
VaR xác định và xem xét khả năng thất thoát vốn cũng như xác suất xảy ra rủi ro đó. Người ta sẽ đo lường bằng cách đánh giá cấp độ tổn thất tiềm năng, xác suất diễn ra trong một khung thời gian nhất định.
VaR xác định và xem xét khả năng thất thoát vốn cũng như xác suất xảy ra rủi ro
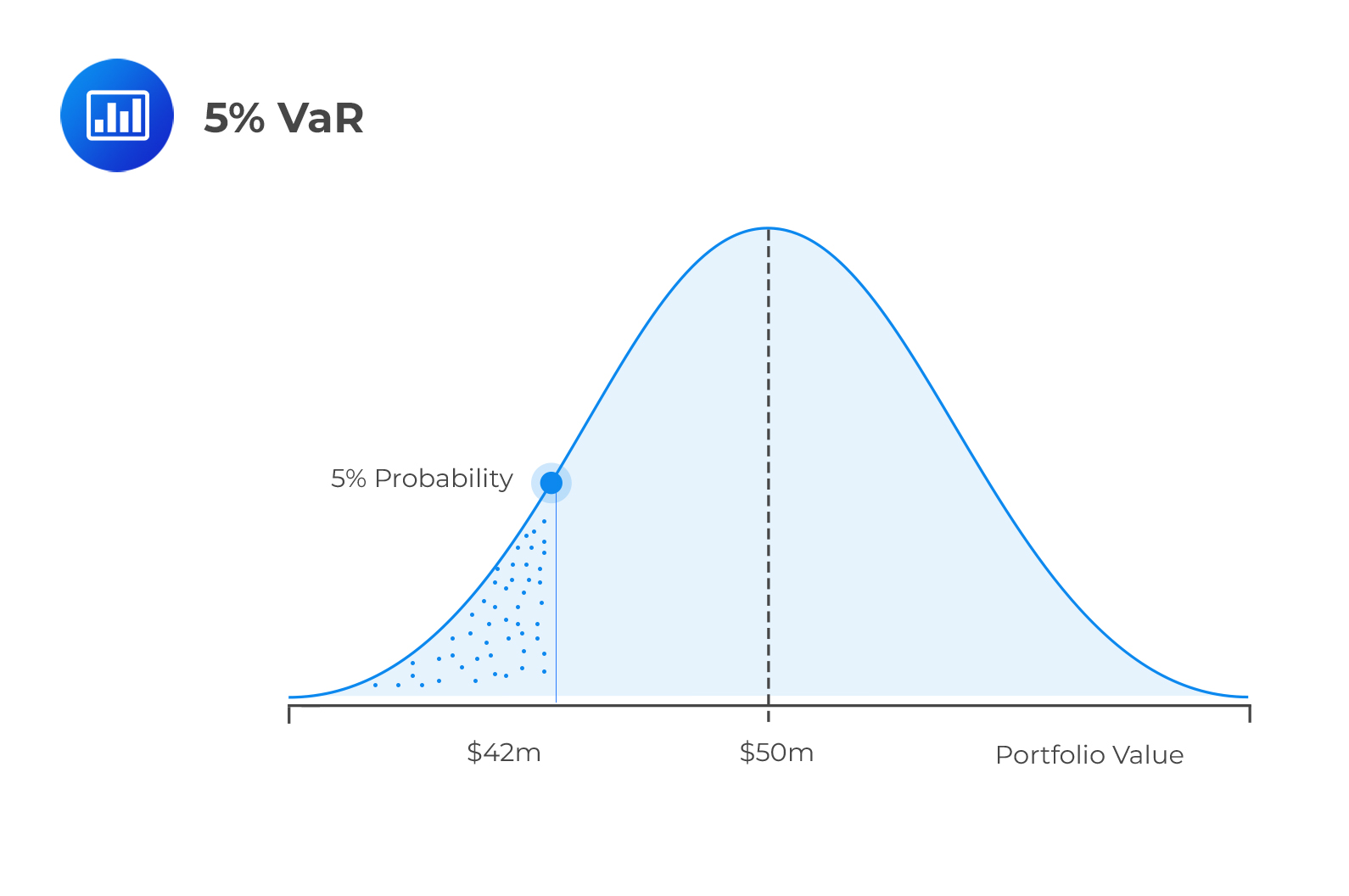
Ví dụ: Bạn có trong tay 1 trái phiếu mệnh giá $1000 đang được giao dịch với giá $700. Giá trị VaR mức 95% của trái phiếu đó trong 1 ngày là $90 - VaR = $90.
Điều này nghĩa là nếu doanh nghiệp phát hành trái phiếu vẫn hoạt động bình thường, trong 1 ngày , với xác suất 95 % , giá trị bạn nắm giữ sẽ giảm nhiều nhất là $90 trong 1 ngày, và trường hợp tệ nhất giảm hơn số tiền đó là 5%.
Những phương pháp ước tính cùng ưu nhược điểm
Hiện nay, Value at Risk có 4 phương pháp đo lường gồm: Phân tích quá khứ(Historical method), RiskMetrics, Phương sai – hiệp phương sai(Variance-covariance method) và Monte Carlo.
Sơ đồ phân tích giá trị chịu rủi ro - Value at Risk
|
Phương pháp |
Ưu điểm |
Nhược điểm |
|
Phân tích quá khứ |
- Được thiết kế và áp dụng khá dễ dàng. - Không cần giả thuyết về quy luật phân bổ. |
- Đòi hỏi có số liệu cực lớn.
|
|
Phương sai - hiệp phương sai và RiskMetrics |
- Được thiết kế và áp dụng khá dễ dàng. - Có thể áp dụng cho danh mục đầu tư bao gồm cả chứng khoán tuyến tính(ví dụ như cổ phiếu). |
- Không đem lại hiệu quả tốt đối với những chứng khoán phi tuyến. - Ít quan tâm đến trường hợp xấu nhất, do đó không chứng minh được giả thuyết về phân bố chuẩn các dữ liệu. |
|
Monte Carlo |
- Khả năng tính VaR vô cùng chính xác. - Có thể áp dụng cho danh mục đầu tư bao gồm cả chứng khoán phi tuyến. |
- Khó chọn được một phân bố xác suất. - Chi phí thực hiện tính toán rất cao. |
Trên đây là toàn bộ thông tin về giá trị chịu rủi ro VaR. Hy vọng rằng qua bài viết của chuyên trang bạn đã có nhiều kiến thức hữu ích. Hãy theo dõi website để không bỏ lỡ những bài đọc sau nha.
Theo: dnppower.com.vn
4.9/5 (97 votes)


